Tag Archives: Wargames

Light at the End of the Tunnel

Wargames, Slopes & the High Ground

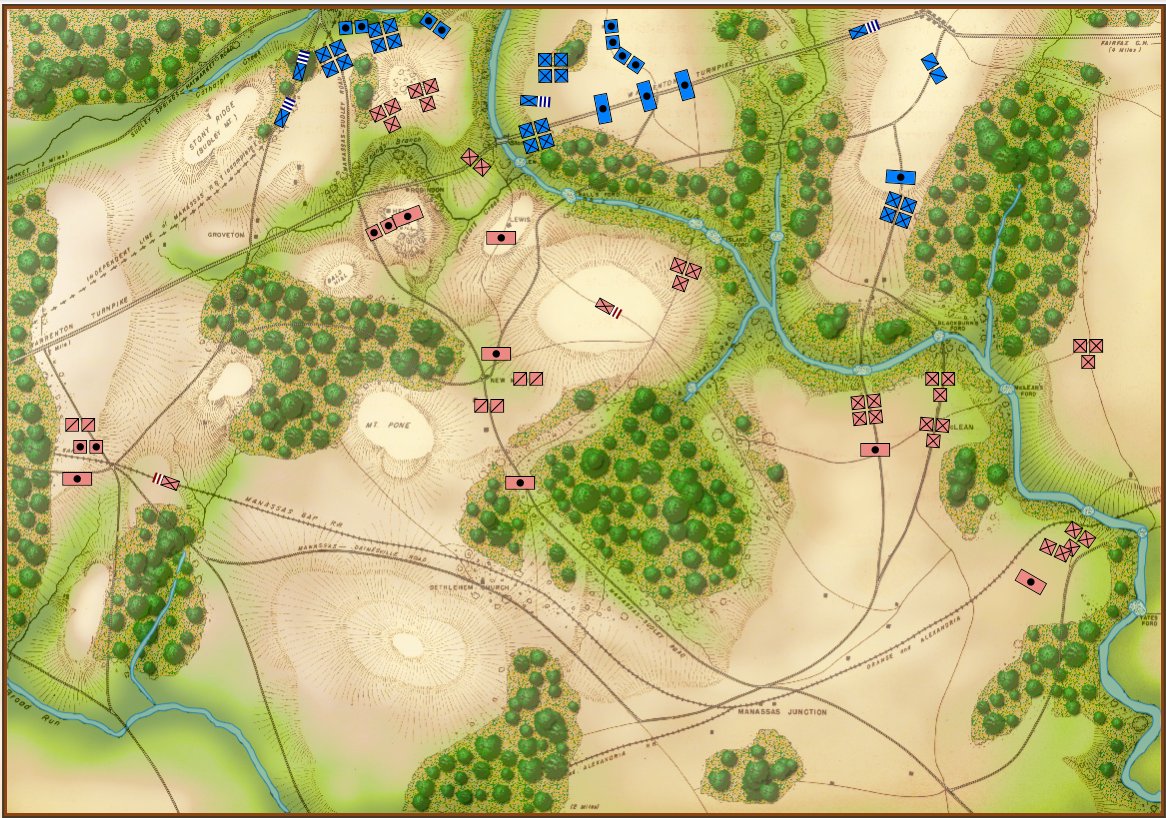
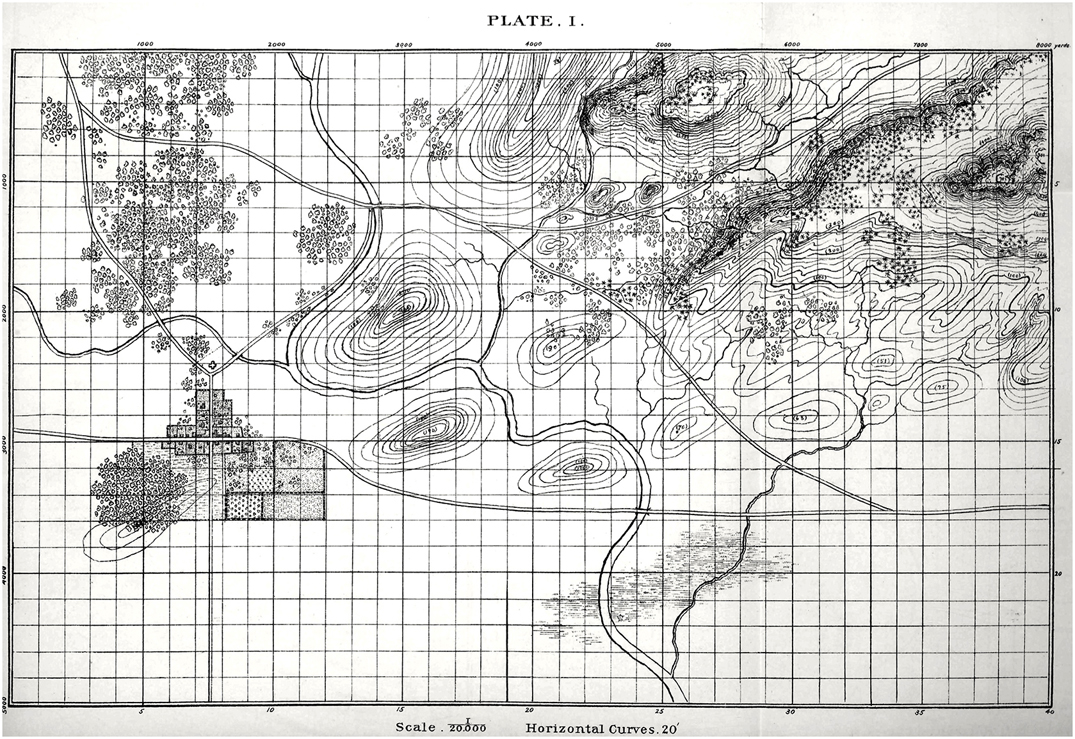
Rules for how slopes effect attack and defense from Avalon Hill’s Gettysburg (1960 edition). Author’s collection. Click to enlarge.

One of the first rules that we all learned when we began to play wargames (at least this was true of early Avalon Hill games for me way back in the 1960s) was that if the defending unit was on a hill and the attacking unit was on the slope, the defender’s ‘defense factor’ was doubled. Under some circumstances, a defending unit could even have its defense factor tripled (see right). And, yes, there were situations (see below) where an enfilading attacking unit could negate the defenders 2:1 advantage. For my entire wargaming life – over fifty years now – this basic rule of thumb applied: a unit on a hill was twice as strong, defensively, than it would be on the plains below. I’ve used this ‘defensive factor multiplier’ in every wargame I’ve designed going back to UMS in the 1980s. I never gave it a second’s thought. Until now.

Detail of rules from Avalon Hill’s Waterloo (1962) showing when a defender’s strength is doubled on a hill and when the effect is negated.

General Staff has no concept of “defense factor.” Think about it, what is a ‘defensive factor’? It seems to act like armor of some sort. It certainly is a valid concept in naval warfare or armored warfare or jousting, but it doesn’t apply in 18th and 19th century warfare that General Staff: Black Powder is designed to simulate. Instead, units in General Staff are weapons platforms. Units project firepower which result in casualties. Indeed, all combat resolution boils down to this equation: How many casualties did this unit inflict on that unit?

Since there is no ‘defensive factor’ to multiply by two for being on a hill defending against an attacker climbing a slope, how or what does General Staff multiply or divide? What is the source for the 2:1 defense factor multiplier for having the high ground? These were the questions that I recently investigated.

It turns out there has been very little research done on the subject of military movement on slopes of various degrees, and the effect of angle of slope on defending a position against a unit attacking up slope. Yes, the U. S. Army has published this on foot marches and slopes but it doesn’t cover 19th century cavalry, artillery, horse artillery, etc.).¹⁾I contacted respected military historian and researcher Brent Nosworthy who wrote back, “The effects of slopes on the speed of movement and the cohesion of troops is a very interesting question indeed. I am enclosing a rough draft of a chapter from The Metrics of War booklet I was working on last year. I think here and there is some information as to how it affected beast of burden’s ability to draw artillery. There were several articles about defending and attacking heights in Rider, John (Editor); British Military Library: A Complete Body of Military Knowledge; second edition, 2 volumes, London, 1798-1801. I cannot remember if there were specific references to these issues in these articles. I also recommend if you have not already consulted: Tielke, Johann Gottlieb, The field engineer; or instructions upon every branch of field fortification: … with plans and explanatory notes. Translated from the fourth … London, 2 volumes, 1789. Russell, John (Lieutenant – 96th Regiment of Foot); A Series of Military Experiments of Attack and Defence, Made in Hyde-Park, in 1802, London, 1806. Adye, Ralph Willet; The Bombardier, and Pocket Gunner, Second Edition, London, 1802. However, I am not certain they contain any references to the effect of the angle of slope on speed and cohesion.”

What I was looking for was a table that cross-indexed angle of slope with its effect on attack, defense and movement. What I found was Table D, (below) from the rules for Charles Totten’s Strategos: The Advanced Game. on the Grogheads.com site:

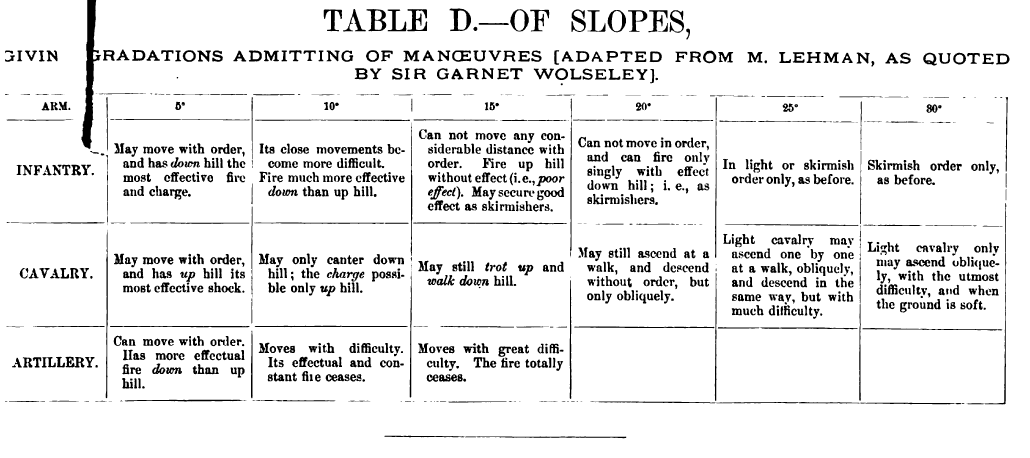
From. “Charles Totten’s Strategos: The Advanced Game.” found at Grogheads.com. Published in 1890.

What this chart shows is:

Unit types respond differently to moving up or down different slopes; e.g. no artillery can ascend a slope greater than 15°, no cavalry can descend a slope greater than 30°, and infantry can only ascend slopes of greater than 30° in skirmish formation.
Having superior elevation does not impart any defensive advantage by itself.
Having superior elevation on a steep slope can actually be a defensive disadvantage; e.g. artillery cannot fire down a 15° slope, and cavalry cannot charge down slopes greater than 15°.
Units firing uphill have increasingly less effect as the angle of slope increases; e.g. infantry has limited or no effect firing uphill at greater than a 20° slope, cavalry cannot charge up a slope greater than 15°, and artillery has no effect when firing up a slope greater 15°. Indeed, this is where the the traditional defensive advantage of holding the high ground derives from: defensive fire is not more effective, rather offensive fire is much less effective when attacking uphill.

If we look at two battles of the American Civil War that are known for assaults up steep slopes (Fredericksburg, December 13, 1862 and Missionary Ridge, November 23, 1863) we find that the values in Table D, above, are largely validated.

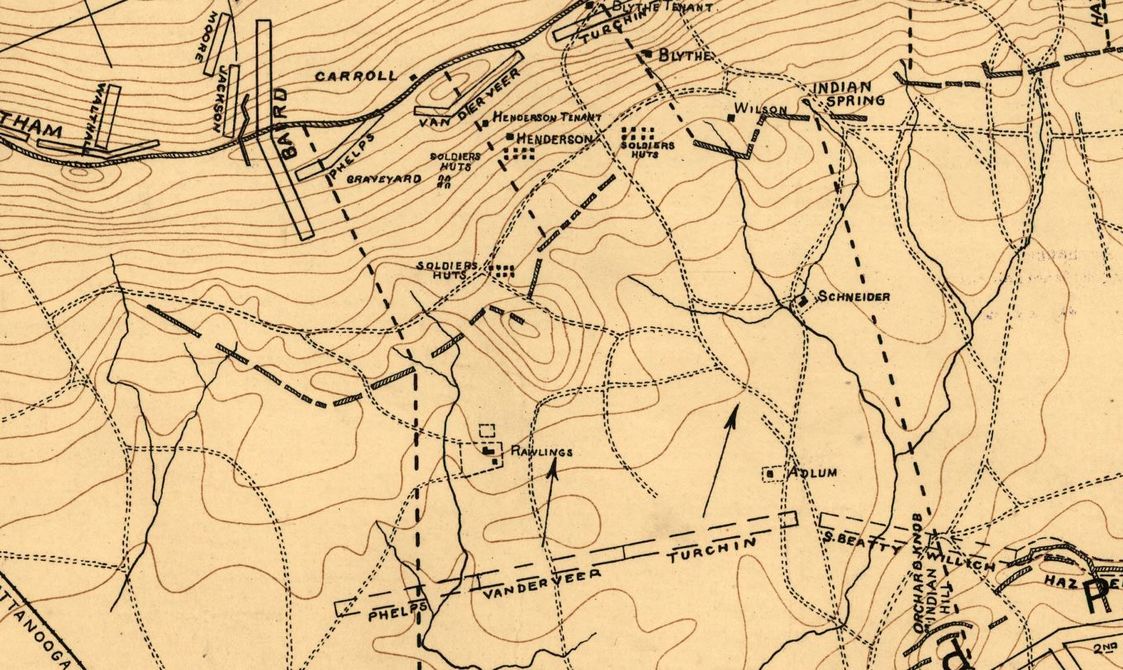
Detail of map of Missionary Ridge from the Library of Congress. The crest of the ridge is about 275 feet above the plain below. In numerous places, the slope is greater than 20°.

The story of the successful Union attack on Missionary Ridge is legendary: Union forces originally assigned to capture the rifle pits at the base of the ridge pushed up the slope without orders, primarily to escape defensive fire from above. They scaled the ridge in a loose, skirmish formation, not firing until they reached the crest.

As we can see from the above map the slope of the Union attack up Missionary Ridge is, at points, greater than 20°. In Brent Nosworthy’s, Roll Call to Destiny: The Soldier’s Eye View of Civil War Battles he writes (page 250), “One of the most notable characteristics of this engagement was the relatively light number of casualties suffered by Van Derveer’s attack force, even though it had to break through two sets of fieldworks.” “To the untrained eye looking at the defenses way up on Missionary Ridge… the Confederate position must have appeared impressive, possibly impregnable, and if not impregnable, then capturable only after the expenditure of many lives. This was the opinion of the Confederate commanders who had chosen to defend the position. (page 252)” “Unfortunately for the Confederates, the military reality was quite the opposite. A high ridge immediately above a steep gradient is one of the worst imaginable defensive positions, about equivalent to placing one’s forces in a line with their back to a river and no avenue of retreat. (page 253). ”

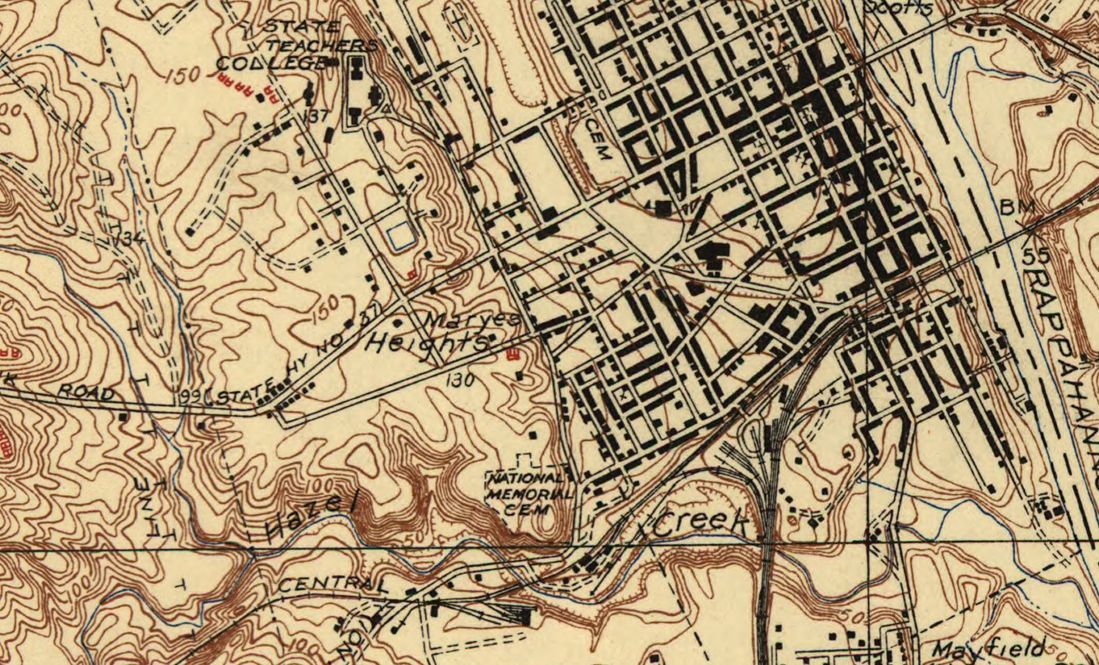
This map of Fredericksburg from the Library of Congress (1931) shows a 90 foot rise in elevation above the plain for Marye’s Heights.

Union forces attacking up the gentler slope at Fredericksburg were not so fortunate. Except in a few steep places that offered shelter from Confederate artillery most of the Union attack was under constant fire. Quoting from Nosworthy’s Roll Call to Destiny (page 129), “a British artist on assignment for the Illustrated London News would recall the effect of the artillery fire on the advancing Union lines: ‘I could see the grape, shell, and canister from the guns of the Washington Artillery mow great avenues in the masses of Federal troops rushing to the assault.'”

Nosworthy, in, The Bloody Crucible of Courage: Fighting Methods and Combat Experience of the Civil War, writes (422-3), “It had long been a general maxim that artillery should only be placed at the top of a slope which it could defend by itself. The artillery had to be able to direct an unobstructed fire against the base of the hill otherwise the enemy force could form in the dead zone and begin its assault up the hill unopposed by the artillery. Officers were cautioned, however, against ever placing artillery on either steep hills or high elevations. Ideally, artillery was placed on elevations whose height was 1% of the distance to the target and were never to be placed upon hills where the elevation was greater than 7% of this distance. When artillery was required to defend a lofty hill or elevation, whose height made it impossible for the artillery to command the base, artillery officers were advised, if at all possible, to place the battery lower along the slope, such as at the halfway point.” The problem of course, was that artillery could not lower the barrels of their guns sufficiently to fire down steep slopes.

Slopes in General Staff

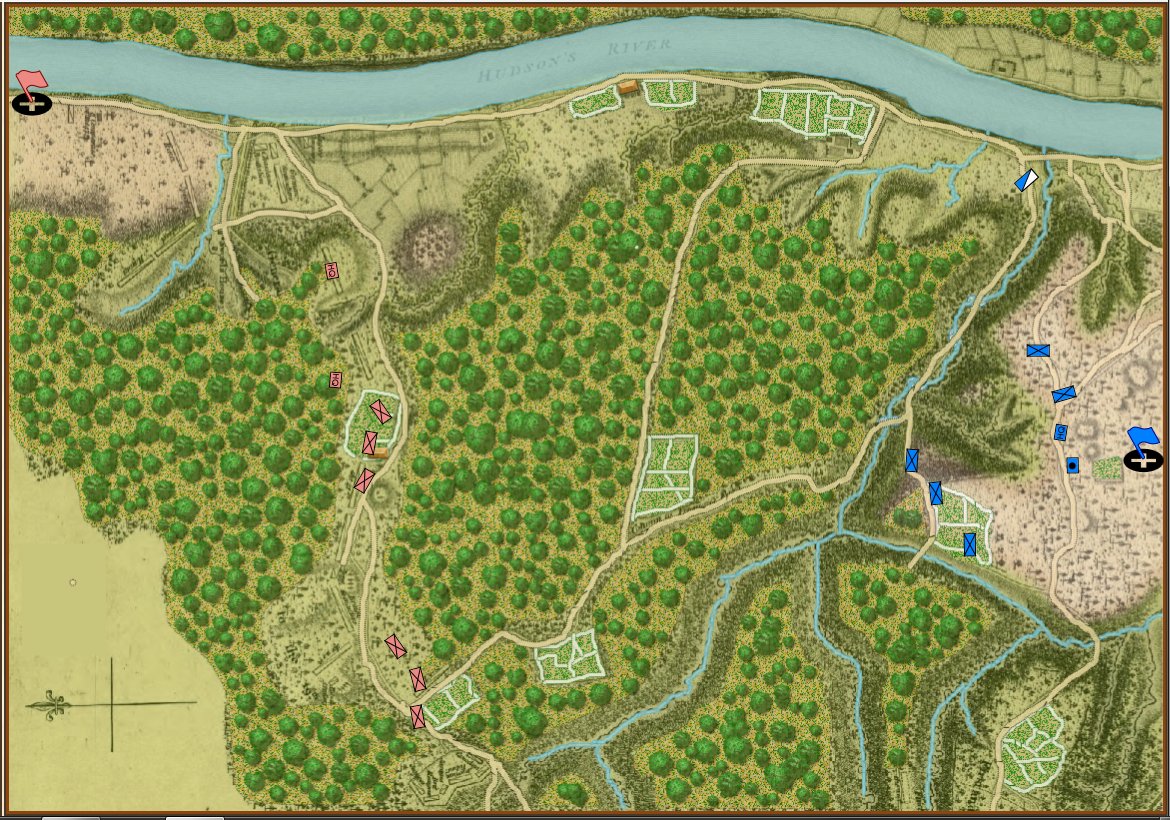
General Staff does not use hexagons or ‘zones’ of any sort. One of the failings of a system using hexes is that the entire hex has one elevation; there are no gradual slopes, just precipitous cliffs. From primary source elevation and topographical maps (like below) three-dimensional battlefields are constructed in the General Staff Map Editor (see below).

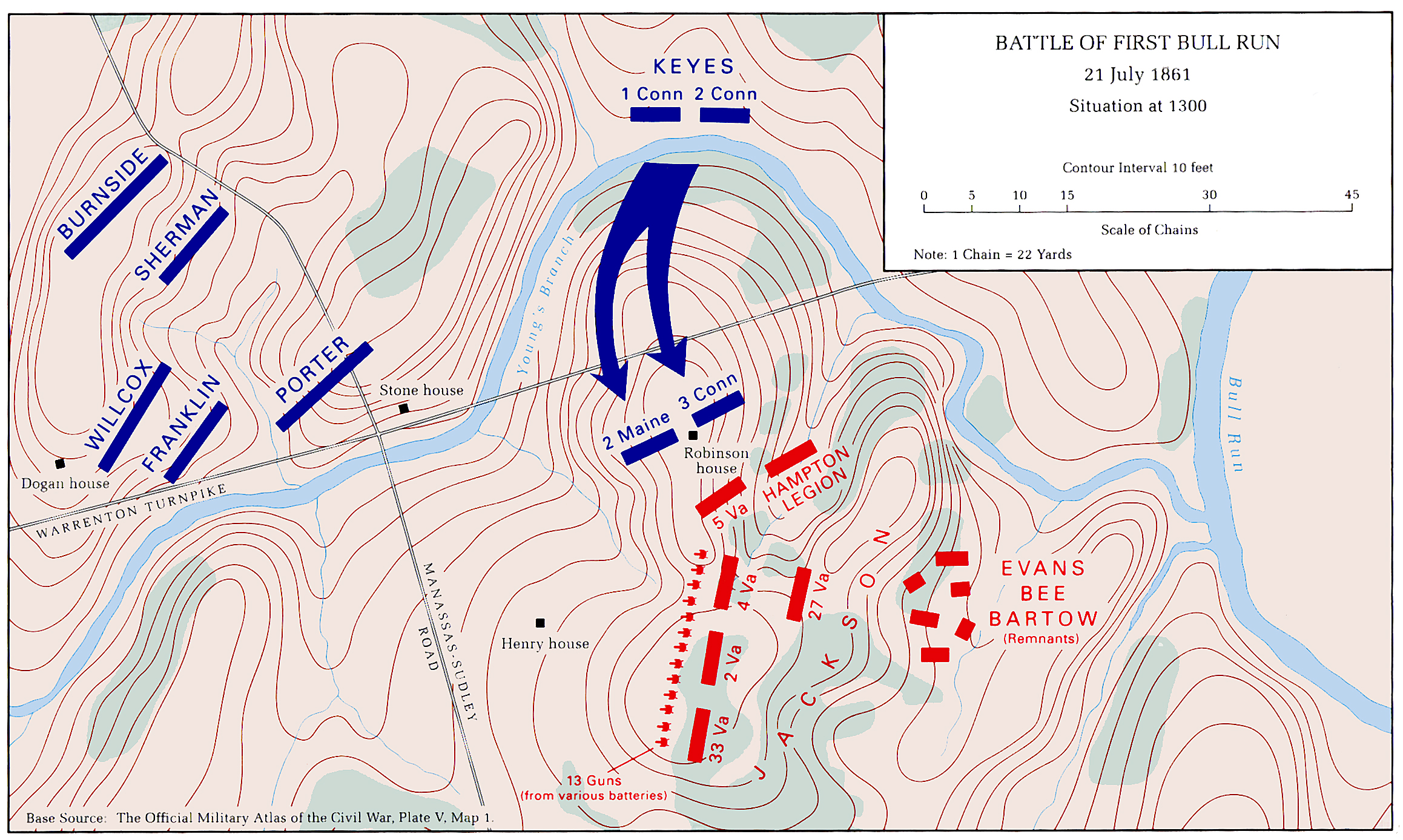
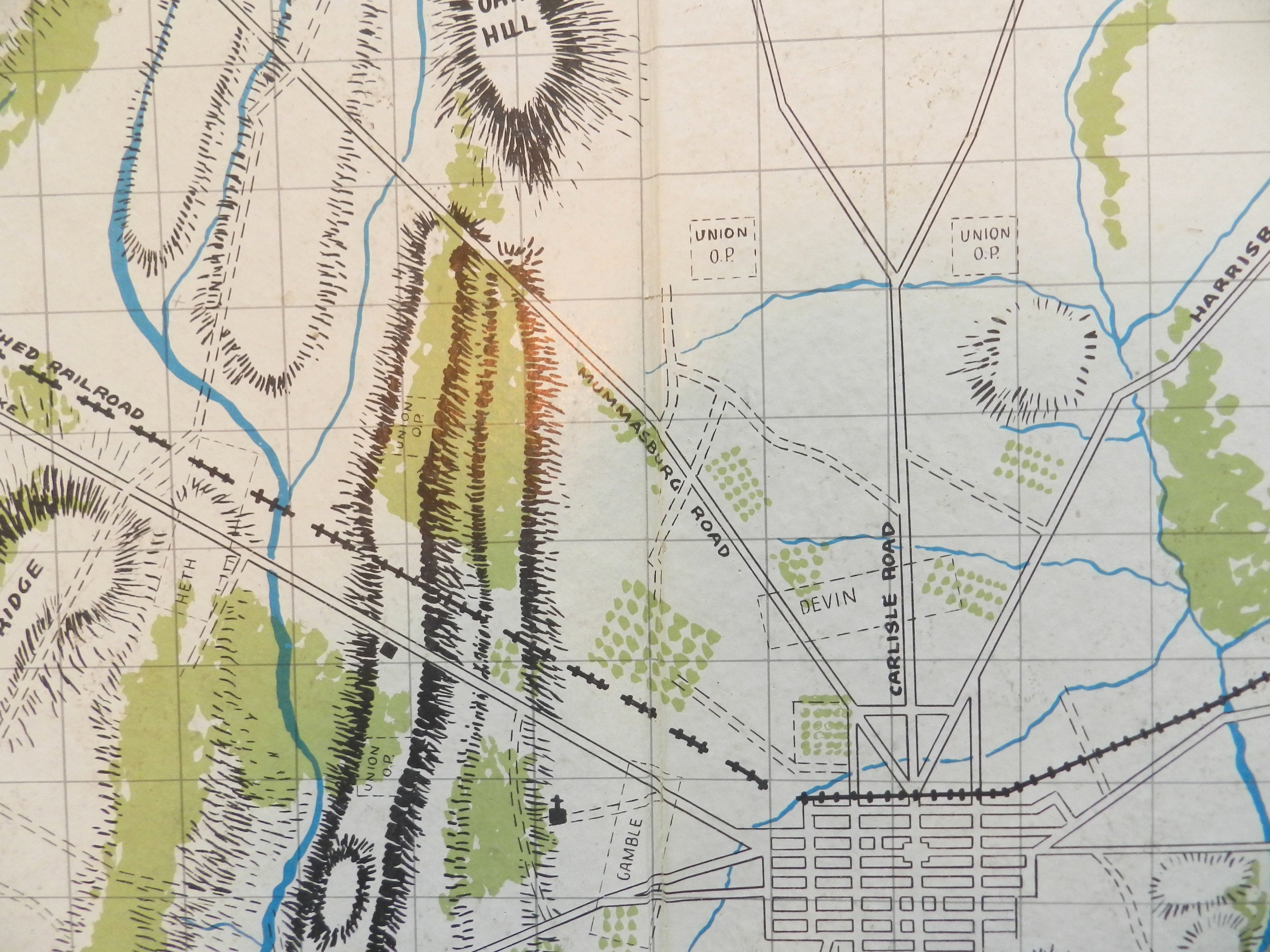
Topographical map with contour lines of Keyes’ attack at the battle of 1st Bull Run. From Wikipedia. Click to enlarge.

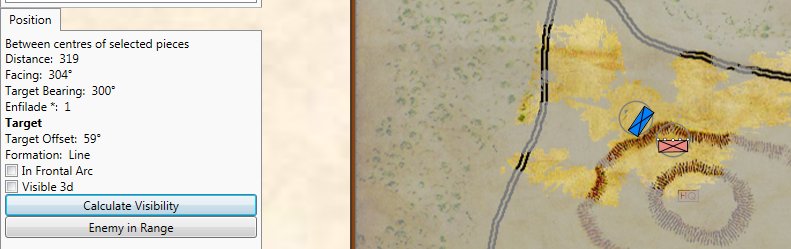
The General Staff Map Editor has a Terrain Visualizer tool (see below). It allows a line to be drawn between any two points on the map and a cross-section of the terrain and elevation to be displayed.

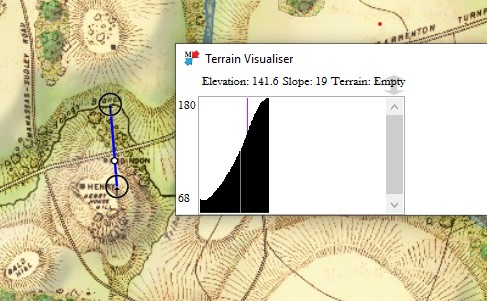
The area of Keyes’ attack in the General Staff Map Editor showing the cross-section Terrain Visualizer with slope calculations along the blue line drawn between the two user selected red circles. The white circle on the blue line is the current point being displayed by the vertical line in the Terrain Visualizer.

In the above image we see that the steepest part of the slope up Henry House hill is 19°. This is confirmed by the contour map, above and a photograph of the actual area below:

This panorama photographic view of the area covered by Keyes’ attack at 1st Bull Run was taken by Johnnie Jenkins December, 2020. The Robinson House was beyond the large tree, center. Click to enlarge.

As always, please feel free to contact me directly (Ezra[at]RiverviewAI.com) if you have any questions or comments.

References[+]

References
↑1	I contacted respected military historian and researcher Brent Nosworthy who wrote back, “The effects of slopes on the speed of movement and the cohesion of troops is a very interesting question indeed. I am enclosing a rough draft of a chapter from The Metrics of War booklet I was working on last year. I think here and there is some information as to how it affected beast of burden’s ability to draw artillery. There were several articles about defending and attacking heights in Rider, John (Editor); British Military Library: A Complete Body of Military Knowledge; second edition, 2 volumes, London, 1798-1801. I cannot remember if there were specific references to these issues in these articles. I also recommend if you have not already consulted: Tielke, Johann Gottlieb, The field engineer; or instructions upon every branch of field fortification: … with plans and explanatory notes. Translated from the fourth … London, 2 volumes, 1789. Russell, John (Lieutenant – 96th Regiment of Foot); A Series of Military Experiments of Attack and Defence, Made in Hyde-Park, in 1802, London, 1806. Adye, Ralph Willet; The Bombardier, and Pocket Gunner, Second Edition, London, 1802. However, I am not certain they contain any references to the effect of the angle of slope on speed and cohesion.”

A Game of Birds & Wolves

Leave a reply

Commander Roberts going over the lessons learned from “The Game.” Photo from, “A Game of Birds and Wolves,” by Simon Parkin.

Simon Parkin’s A Game of Birds and Wolves: The Ingenious Young Women Whose Secret Board Game Helped Win World War II, tells the fascinating story of a wargame created during the height of the U-Boat Atlantic campaign to be used as a testbed for discovering new anti-submarine tactics. In early 1941, when German wolf packs were destroying Allied shipping at a devastating rate, British Naval Commander Gilbert Roberts was taken out of retirement and personally ordered by Winston Churchill to, “Find out what is happening and sink the U-boats.”

Roberts was given the top floor of the Western Approaches HQ in Liverpool and a small group of WRENs (Women’s Royal Naval Service) as assistants to invent tactics that would counter the enemy wolf packs. His project would be called the Western Approaches Tactical Unit (WATU). (The Western Approaches HQ in Liverpool is now a museum and I can’t wait to visit it when this pandemic is over and General Staff is finished.)

The WATU project – known simply as, “The Game,” – is not the first example of a wargame used as a testbed to discover and improve combat maneuvers. Indeed, Scotsman John Clerk, wrote, An Essay on Naval Tactics: Systematical and Historical in 1779 after using, “…a small number of models of ships which, when disposed in proper arrangement, gave most correct representations of battle fleets… and being easily moved and put into any relative position required, and thus permanently seen and well considered, every possible idea of a naval system could be discussed without the possibility of any dispute.” Using these models Clerk proposed the tactic of “cutting the line,” that Nelson employed at Trafalgar¹⁾https://en.wikipedia.org/wiki/John_Clerk_of_Eldin. Nelson would quote from Clerk’s essay in his famous Trafalgar Memorandum.

When Roberts reported to Sir Percy Noble, commander of Western Approaches he explained that he intended to, “develop a game that would enable the British to understand why the U-boats were proving so successful in sea battles and facilitate the development of counter-tactics… The game would become the basis for a school, where those fighting at sea could be taught the tactics. With a few adjustments.. [the] wargame could be used for either analysis or training.”²⁾A Game of Birds and Wolves, p. 143 Not surprisingly, Roberts was met with skepticism and not a little bit of derision. As one who is constantly pitching the importance of wargames to the U. S. military I understand the uphill fight that Roberts was facing. British destroyer commanders definitely did not want to go to Liverpool to, “play a game.” But, since the orders had come directly from Churchill, Noble had little choice but to give Roberts the top floor of the Western Approaches HQ for his ‘game’. Roberts made a tactical mistake by referring to WATU’s ‘product’ (in modern bureaucratic parlance) as a ‘game’. I learned this early on in my career: never say the word ‘game’ if it can be avoided. Call what you’re working on a ‘simulation’. Chess is a game. Risk is a game. But I write simulations; and clearly what Roberts was working on was a simulation, too. (That said, the phrase, “game it out,” has now passed into the common idiom and is synonymous with ‘simulation’.)

WATU simulated Fog of War by requiring the users to view the board through peep holes cut in canvas drapes. Submarine tracks (see above) were drawn in green chalk which, apparently, was not visible from the other side of the canvas sheets. The photo shows British destroyer commanders playing, “The Game,” and learning from the simulation. Photo from, “A Game of Birds and Wolves.”

In order to simulate Fog of War Roberts invented a system in which the destroyer commanders would view the board from behind a canvas sheet; their view of the battle restricted by peep holes cut in the canvas. Furthermore, submarine tracks were drawn with green chalk on the floor (see above photo) which, somehow, became invisible when viewed from the other side of the canvas. Consequently, the destroyer commanders had only a restricted view of the battle around them and were completely in the dark as to the simulated U-boats positions.

When Roberts began his work nobody in the British Admiralty knew U-boat tactics. Indeed, the German U-boat commanders were creating their tactics on the fly often ignoring the Kriegsmarine’s Memorandum for Submarine Commanders to fire torpedoes at no closer than 1,000 meters. U-boat ace, Otto Kretschmer was the first to insist that the most efficient way to attack convoys was to slip inside the destroyer screen, launch torpedoes at a range of about 500 meters, submerge and wait for the convoy to pass over them to make his escape ‘out the back’ of the convoy. Interestingly, this was the same technique that I discovered playing Sierra On Line’s Aces of the Deep.

One of the first scenarios that Roberts investigated using his new wargame was the battle of Convoy HG 76. This was a multi-day contest involving 32 merchant ships, 24 escorts and 12 U-boats. It was considered a great Allied victory because five U-boats were sank (though the Allies only knew of three at the time) and 30 merchant ships made it home safely. Assisted by WRENs Jean Laidlaw and Janet Okell, they replayed the historical situation hoping to understand Allied commander Captain Frederick John “Johnnie” Walker’s anti-submarine maneuver ‘Buttercup’. The Buttercup maneuver (named after Walker’s pet name for his wife) involved, “on the order Buttercup… all of the escort ships would turn outward from the convoy. They would accelerate to full speed while letting loose star shells. If a U-boat was sighted, Walker would then mount a dogged pursuit, often ordering up to six of the nine ships in his [escort] group to stay with the vessel until it was destroyed.”³⁾A Game of Birds and Wolves, p. 155

What confused Roberts was that the Allied merchant Annavore was torpedoed while in the center of the convoy. As he and the WRENs replayed the scenario they could not duplicate reality unless the U-boat had, “entered the columns of the convoy from behind. And it must have done so on the surface, where it was able to travel at a faster speed than the ships. By approaching from astern, where the lookouts rarely checked, the U-boat would be able to slip inside the convoy undetected, fire at close range, then submerge in order to get away.”⁴⁾The Game off Birds and Wolves. P. 158

Using the scenario of when the escorts actually sank a U-boat using the Buttercup maneuver it was determined that they had succeeded by only accidentally hitting a U-boat that was joining the attack on the convoy and not the actual U-boat who had made the attack that they were pursuing. This makes sense when you realize that the attacking U-boat had submerged immediately after the attack and was waiting for the remaining convoy to pass overhead while the escorts were running far outside the perimeter of the convoy looking for it.

In other words, Walker’s Buttercup maneuver was, in fact, a terrible anti-submarine tactic.

The ‘Raspberry Maneuver’, created from numerous runs of ‘The Game’ was determined to an effective anti-submarine tactic. Here it is drawn by Admiral Usborne. From the book, “A Game of Birds and Wolves.” Click to enlarge.

The first successful anti-submarine tactic to be invented using the Game as a test bed was, “Raspberry,” (so called by Wren Ladlaw as a ‘raspberry‘ to Hitler). As you can see from the above drawing, upon discovery of a U-boat or a torpedo hit, the escorts draw closer to the convoy, not the opposite as in Walker’s Buttercup maneuver. When Roberts and the WRENs ran a scenario for Western Approaches commander Noble and his staff, Noble – who at first was highly skeptical – was so impressed that he immediately sent a message to Churchill, “The first investigations have shown a cardinal error in anti-U-boat tactics. A new, immediate and concerted counter-attack will be signaled to the fleet within twenty-four hours.” ⁵⁾The Game of Birds and Wolves, p. 162 By summer of 1942, using these new maneuvers, U-boat losses had quadrupled. Eventually other anti-U-boat maneuvers were also developed by the WATU team and all Atlantic destroyer commanders were ordered to WATU to play, “The Game,” and learn the lessons.

Obviously, there were other improvements in anti-submarine warfare that also contributed to the Allies winning the Battle of the North Atlantic. Nonetheless, it is interesting to read about the proper application of simulations in wartime. I have long been an advocate of simulations to test, “what if” scenarios. Indeed, this has been the main focus of my professional career for thirty plus years. It’s still an uphill battle.

References[+]

References
↑1	https://en.wikipedia.org/wiki/John_Clerk_of_Eldin
↑2	A Game of Birds and Wolves, p. 143
↑3	A Game of Birds and Wolves, p. 155
↑4	The Game off Birds and Wolves. P. 158
↑5	The Game of Birds and Wolves, p. 162

Introducing a New Generation to Wargames

26 Replies

My childhood friend, Carl Hoffman, introduced me to Avalon Hill wargames. Carl is now a history teacher.

It was my good friend, Carl Hoffman, who lived across the street when I was about 10, who introduced me to Avalon Hill (AH) wargames. The AH wargames of the 1960s were perfectly suited to spark a kid’s imagination. The rules were easy to understand (four pages, big type, with illustrations explaining movement and combat), the Combat Results Table (CRT) was straightforward (and taught us to calculate ratios, too), and we could refight Gettysburg or Waterloo on a rainy afternoon. We learned history (Carl became a history teacher) and problem solving (I became a computer scientist). I’m sure many of us had similar experiences forty or fifty years ago.

For a long time I’ve felt that there is a need for similar ‘introductory wargames’ to engage the next generation of grognards and wargamers. While the hardcore aficionados want more complex and detailed games I’ve also understood that we needed simple, introductory games, to entice a new generation. From the beginning, I have always had a simpler wargame embedded inside of General Staff. Specifically, if we remove all the layers of historical simulation, what remains is a simple introductory wargame.

The Layers of Historical Simulation in General Staff

Each layer of historical simulation can be turned on or off when playing a General Staff scenario. The more options you add, the more historically accurate the simulation becomes. The options are:

Unit strength
1. Unit strength is a value from 1 – 4 with units being reduced in steps.
2. Unit strength is the actual historic number of troops and every individual casualty is tracked.
Combat resolution
1. Simple Combat Resolution Table like the old AH CRT.
2. Complex Combat Resolution Equation taking into effect morale, experience, leadership, terrain, and elevation.
Moving units
1. Units are moved directly by the player.
2. Orders to move units are issued down a chain of command from the top HQ to the subordinate HQ via couriers and the rapidity with which the orders are executed depends on the Leadership Value of the subordinate HQ and subordinate units.
Fog of War (FoW)
1. No Fog of War. The entire map is visible and all units (friend and foe) are displayed on it.
2. Partial FoW. The entire map is displayed and the sum of what all friendly units can see is displayed.
3. Complete FoW. You see only what the commander can see from his HQ and nothing else. All unit positions not directly observable are updated via couriers and are frequently no longer accurate by the time the courier arrives.

So, at it’s most complex (let’s call this a Historical Accuracy level of 100%) this is what the player commanding the Army of the Potomac (Blue) would see (what General George McClellan could actually see through his telescope on the lawn of the Pry House on the morning of September 17, 1862):

Antietam from the perspective of General George B. McClellan at the Pry House on the east bank of the Antietam Creek. This is complete Fog of War and the highest level of historical accuracy. Screen shot. Click to enlarge.

And, interestingly, this view of what McClellan could see is confirmed in The U. S. Army War College Guide to the Battle of Antietam and The Maryland Campaign of 1862 edited by Jay Luvaas and Harold W. Nelson.”General McClellan and his headquarters staff observed the battle from the lawn of the Pry House… Through a telescope mounted on stakes he enjoyed a panorama view of the fighting… He could see Richardson’s division break through the Confederate position at the Bloody Lane. He could not, however, follow the movements of the First and the Twelfth Corps once they disappeared into the East Woods, which masked the fight for the Cornfield, nor did he witness the attempts to seize Burnside’s bridge to the south because the view from the Pry House was blocked by trees and high ground.” – p. 119.

So, the above is the 100% historically accurate view of the battle of Antietam from McClellan’s Headquarters. This is the ‘introductory’ view:

Antietam in ‘Introductory’ mode. Note that unit strengths are represented by one to four icons. Also note the lack of HQs. Screen shot. Click to enlarge.

I first saw the concept of ‘unit steps’ in Jim Dunnigan’s Avalon Hill classic, 1914 and I’m shamelessly using it here. I very much like the simplicity of this system: as units take casualties, they are reduced, in steps, from four icons, to three, to two, etc. I also very much like the idea that this is not an abstraction of the battle of Antietam (or Little Bighorn, or Quate Bras, etc.) but the actual units in their actual locations. This fulfills my requirements for an introductory wargame: historic, teaches tactics and problem solving, easy to play, simple rules, quick to learn and quick to play (I would think a game could easily be played in less than an hour).

Here are some more General Staff scenarios in ‘introductory mode’:

1st Bull Run, 11:30 hours, ‘introductory’ mode. Screen shot. Click to enlarge.

Little Bighorn in ‘introductory’ mode. Screen capture. Click to enlarge.

Quatre Bras in ‘introductory’ mode. Screen capture. Click to enlarge.

I could use your help! Announcing a ‘name the mode’ contest!

From ‘The American Kriegsspiel. Clicking on this image will take you to the Grogheads.com article on William Livermore’s American Kriegsspiel.

I originally called ‘introductory’ mode, ‘Kriegsspiel’ mode because I was reminded of the maps and blocks that Kriegsspiel uses. However, I pretty quickly received some emails from the Kriegsspiel community complaining – and rightfully so – that Kriegsspiel isn’t an introductory game. Absolutely! And if you’ve ever taken a look at the original rule books and tables you would agree, too.

So, here’s my problem (and how YOU can help): I need a new phrase to replace ‘Kriegsspiel mode’. I’ve been using ‘Introductory mode’ but I just don’t like it. I really need a new name for this version. I’m open to any suggestions. How about a completely made up word? ‘Stratego’ would be great if it hadn’t already been used. So, I’m announcing a contest to ‘name this mode’. The winner will receive 2 General Staff coffee mugs. Please email me (Ezra@RiverviewAI.com) with you suggestions. Thank you for your help!

The Problem With Hexagons

38 Replies

Hexagons are ubiquitous in wargames now (indeed, both Philip Sabin’s War: Studying Conflict Through Simulation Games and Peter Perla’s The Art of Wargaming feature hexagons on their book covers), but this wasn’t always the case. My first wargame – the first board wargame for many of us – was Avalon Hill’s original Gettysburg (by the way, $75 seems to be the going price for a copy on eBay these days).

No hexagons in Avalon Hill’s original Gettysburg. Remember how the map contained the original starting positions for the Union cavalry and out posts? From author’s collection. (Click to enlarge)

The American Kriegsspiel by Captain Livermore (circa 1882) only had a map grid for estimating distances. We also have a map grid in General Staff to facilitate estimating distances but you can turn the map grid on or off.

Plate 1 from The American Kriegsspiel by Captain Livermore. Click to enlarge. This image is from GrogHeads wonderful blog post on Nineteenth Century Military War Games. Link: http://grogheads.com/featured-posts/5321

And how about this picture from the Naval War College (circa 1940s)? I just needed an excuse to post this photograph:

A Fletcher Pratt Naval War Game in progress. I never understood why they didn’t use upside down periscopes to check broadside angles rather than getting down on the floor. Click to enlarge. From this blog http://wargamingmiscellany.blogspot.com/2016/02/simulating-gunfire-in-naval-wargames.html

It is pretty common knowledge among the wargaming community that Avalon Hill’s owner, Charles Roberts, introduced hexagons to commercial wargaming in the early 1950s .

“Later, he [Roberts] saw a photograph of one of the RAND gaming facilities and noted they were using an hexagonal grid. This grid allowed movement between adjacent hexagons (or hexes, as they are more frequently called) to be equidistant, whereas movement along the diagonals in a square grid covered more distance than movement across the sides of the squares. Roberts immediately saw the usefulness of this technique and adopted to his subsequent games.”

– The Art of Wargaming, Perla, p. 116

In researching how the RAND Corporation – a major post-war defense think tank – came up with the original idea of employing hexagons to simplify movement calculations (as well as the invention of the Combat Resolution Table or CRT) I stumbled upon an amazing document: Some War Games by John Nash and R. M. Thrall (Project RAND, 10 September 1952; available as a free download here). Yes, that is THE John Nash; A Beautiful Mind John Nash; the Nobel Prize recipient John Nash. The Some War Games summary states:

“These games are descendants of the one originally instigated by A. Mood, and are both played on his hexagonal-honey comb-pattern board. – Some War Games Nash & Thrall.

But what appears on Page 1A of Some War Games is even more exciting:

The earliest reference of using hexagons for wargames. “The board is a honeycomb pattern of hexagonal “squares,” the same that was used in Mood’s game” – From Some War Games (Project RAND, Nash & Thrall).

Sadly, I have been unable to find an actual copy or documentation for “Mood’s game,” but did discover that A. Mood was a statistician who wrote the popular text book, “Introduction to the Theory of Statistics,” and, during World War II was involved with the Applied Mathematics Panel and the Statistical Research Group. Mood was also the author of, “War Gaming as a Technique of Analysis,” September 3, 1954 which is available as a free download here. Unfortunately, I have yet to uncover any images of Mood’s original war game and the very first use of his ‘honeycomb pattern’ board.

Let’s take a quick look at the math behind hexagons:

The cost of moving diagonally as opposed to horizontally or vertically on a map board (from a slide in my PhD Qualifying Exam on least weighted path algorithms).

The problem of quick and easy movement calculation (as shown in the above graphic) is caused by the Pythagorean Theorem. Well, not so much caused, as a result of the theorem:

The distance to a diagonal square, d, is the square root of the square of the hypotenuse (the side opposite the right angle) which is equal to the sum of the squares of the other two sides. We all learned this watching the Scarecrow in the Wizard of Oz, right?

In other words, if everybody could just multiply by 1.41421356 in their heads we wouldn’t even need hexagons! The downside, of course, is now we’ve restricted our original eight axes of movement to six. And there’s another problem; what I call the, “drunken hexagon walk.”

An example of “drunken hexagon walk” syndrome. All we’re trying to do is go in a straight line from Point A to Point B and from Point A to Point C.

In the above diagram we just want to travel in a straight line from Point A to Point B. It’s a thirty degree angle. What could be simpler? How about traveling from Point A to Point C? It’s a straight 90 degree angle. It’s one of the cardinal degrees! What could be simpler than that? Instead our units are twisting and turning first left, then right, then left like a drunk stumbling from one light post to another light post across the street. In theory the units are actually traversing considerably more terrain than they would if they could simply travel in a straight line. This is the downfall of the hex: sometimes it simplifies movement; but just as often it creates absurd movement paths that no actual military unit would ever take.

So, what’s the solution? Clearly, there is no reason why a computer wargame should employ hexes. Computers are very good at multiplying by 1.41421356 or any other number for that matter. Below is a screen shot of General Staff:

Screen shot of General Staff (2nd Saratoga) based on the map of Lt. Wilkinson, “showing the positions of His Excellency General Burgoyne’s Army at Saratoga published in London 1780) . Click to enlarge.

What’s missing from the General Staff screen shot, above? Well, hexes, obviously. Units move wherever you tell them to in straight lines or following roads precisely if so ordered. And units can obviously face in 360 degrees. Consider this screen shot from the General Staff Sandbox where we’re testing our combat calculations:

Screen shot from the General Staff Sandbox. Notes: 3D unit visibility is turned on, displayed values: unit facing, distance, target bearing, enfilade values, target offset. Click to enlarge.

For board wargames hexagons seem to be a necessary evil unless you want to break out the rulers (that never stopped us with the original Gettysburg or Jutland). But, when it comes to computer wargames, I just don’t see the upside for hexagons but I do see a lot of downside. And that’s why General Staff doesn’t use hexes.